
Fig. 1: The bucky2 mesh and 3 different isosurfaces
In the domain of scientific visualization, isosurfaces are a standard way to visualize a scalar field (see fig. 1).

Fig. 1: The bucky2 mesh and 3 different isosurfaces
A typical CUDA GPU like the GTX280 is composed of 30 multiprocessors (MP). Each MP contains 8 scalar or stream processors (SP) working in SIMD. All of the SPs in a MP must execute the same instruction. If all SPs are not in the same execution path, some execute while others wait.
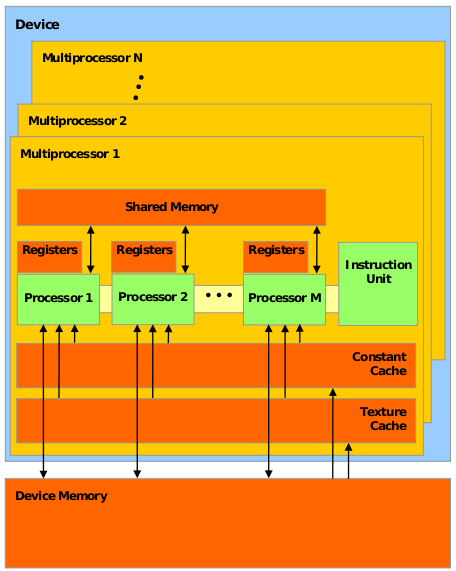
Fig. 2: Architecture of a CUDA capable GPU
The marching tetrahedra (MT) algorithm is the standard way of extracting an isosurface from a tetrahedral mesh. It consists in computing for each cell the intersection between that cell and the isosurface. Depending on how the isosurface intersects the cell 0,1 or 2 triangles are generated (see fig 3). This algorithm is well suited for a GPU parallelization as it can be decomposed in m independant tasks, one for each cell. We already implemented this algorithm in CUDA. The main issue is in the writing of the triangles. For now, we allocate an array capable of storing 2 triangles by cell although in practice an isosurface is composed of a lot fewer triangles (typically many cells are not in the isosurface and do not generate any triangles). Thus the resulting array have lots of holes in it.
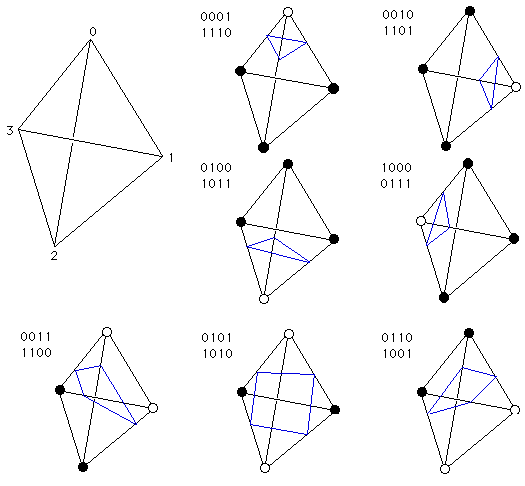
Fig. 3: Marching Tetrahedra
To avoid this problem, we propose an algorithm in 3 phases. In the first phase, we compute the number of triangles generated by each cell. In the second phase, we compute for cell i, the number of triangles generated by all cells whose indices are below i. By doing so, we know in the third phase how much space we need for the output array and where to write the triangles generated by each cell. Another benefit of the 3 phases algorithm is that cells generating 1 triangle and cells generating 2 triangles can be treated separately. This way, SPs that treats cell generating only one triangle do not have to wait for SPs that treats cell generating two triangles. This algorithm has two advantages over the previous one: a smaller memory requirement and a better usage of the SPs in each MP.
The goal of this work is to implement the 3 phases algorithm in CUDA and to compare it with the basic MT implementation. The operation realized in phase 2 is called a prefix (sometimes scan or partial sum). This operation has been implemented in CUDA in the library Cupp. As an efficient implemtation of the prefix on GPU is tricky, the library implementation should be used.
| [1] | CUDA courses. CUDA ZONE |
| [2] | Cudpp library. Cudpp |
| [3] | Shane Ryoo, Christopher I. Rodrigues, Sara S. Baghsorkhi, Sam S. Stone, David B. Kirk, and Wen mei W. Hwu. Optimization principles and application performance evaluation of a multithreaded gpu using cuda. In PPoPP '08: Proceedings of the 13th ACM SIGPLAN Symposium on Principles and practice of parallel programming, pages 73-82, New York, NY, USA, 2008. ACM. |
| [4] | Andr Gu ziec and Robert Hummel Exploiting Triangulated Surface Extraction Using Tetrahedral Decomposition. In IEEE Transactions on Visualization and Computer Graphics. [.pdf ] |